What is Ellipse?

In geometry, an ellipse is a set of those points such that the distances from two fixed points on a plane remain constant. These two fixed points are called foci. The fixed distance is called the directrix of the ellipse. The centre of the ellipse is the midpoint of the line segment joining the two fixed points. The eccentricity of the ellipse is the constant ratio of focal length and length of the semi-major axis. 

An ellipse is shaped like an oval shape, and thus, it is not considered a circular shape. Whereas a circle is a shape that has a set of points at a fixed distance from the centre. Since there are two focus points for an ellipse, there are two lines of symmetry or axes of symmetry, major axes and minor axes. The major axis is the longer chord that passes through the foci of the ellipse, and the endpoints lie on the ellipse. The minor axis is the smaller one, passing through the centre of the ellipse and is perpendicular to the major axis.

An ellipse can likewise be characterised as a conic segment got by the crossing point of a cone with a plane that isn’t perpendicular to the axis of symmetry and also does not intersect the base of the cone.

Some Properties of Ellipse

The following are the basic properties of an ellipse that define it:

• There are two focal points for an ellipse
• There are two symmetrical axes for an ellipse, major axis and minor axis
• An ellipse is always oval in shape
• The eccentricity of the ellipse lies between 0 and 1
• The fixed distance between two focal points is called the directrix
• The area of an ellipse is equal to the πab, where a is the semi-major axis and b is the semi-minor axis
• The length of the latus rectum of an ellipse is given by 2b2/a

Equation of Ellipse

The equation of the ellipse that is centred at (0,0) and has the major axis along the x-axis is given by:

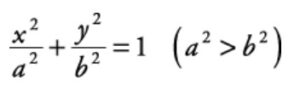
And, if the major axis of an ellipse is along the y-axis, then the standard form of the equation for an ellipse is given by:

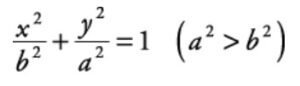
Where 2a is the length of the major axis and 2b is the length of the minor axis. Hence, the endpoints of the major axis are (a,0) and (-a,0), whereas the endpoints of the minor axis are (0, b) and (0, -b). 

Intercepts of Ellipse

As discussed earlier, the equation of the line is based on the length of the major axis and minor axis. Intercept are usually defined for the straight lines in Mathematics. But in the case of the ellipse, intercepts are formed by the major and minor axis of an ellipse. The coordinates of the major axis, i.e., (a,0) and (-a,0), are said to be major intercepts. Similarly, the coordinates of the minor axis, (0, b) and (0, -b), are said to be minor intercepts. 

Focus of Ellipse

Suppose (c, 0) and (0, -c) are the locations of the foci of the ellipse. Then, the value of c can be evaluated using the formula:

c2 = a2 – b2

Where a is the semi-major axis and b is the semi-minor axis.